Lecture 4: Rootfinding and Interpolation

Topics

• Root finding
• Interpolation
• Curve building

$\renewcommand{bs}{\boldsymbol}$

Rootfinding

• The Bible: the love of money is the root of all evil
• Mark Twain: the lack of money is the root of all evil
• Ayn Rand：money is the root of all good

Common rootfinding methods

Search the root of a scalar function $f(x) = 0$, common methods:

• Bisection
• Secant
• Newton-Ralphson
• Brent

Illustrative Examples:

• compute the implied volatility of a call option.
• a more challenging problem of $\Phi(x) + .05x - 0.5 = 0$

from scipy.stats import norm
lecture = 4

# black scholes call
def bs_call(r, s, k, sigma, t) :
    d1 = (math.log(s/k) + (r + .5*sigma*sigma)*t)/sigma/math.sqrt(t)
    d2 = d1 - sigma*math.sqrt(t)
    return norm.cdf(d1)*s - norm.cdf(d2)*k*math.exp(-r*t)

# black scholes vega
def bs_vega(r, s, k, sigma, t) :
    d1 = (math.log(s/k) + (r + .5*sigma*sigma)*t)/sigma/math.sqrt(t)
    return math.sqrt(t)*s*norm.pdf(d1)

f = lambda s : bs_call(r=.05, s=100, k=150., sigma=s, t=1) - 1.
g = lambda s, foo, bar : bs_vega(r=.05, s=100, k=150., sigma=s, t=1) 
f2 = lambda x : norm.cdf(x) + .05*x - .5
g2 = lambda x, a, b : norm.pdf(x) + .05

fig = figure(figsize=[12, 3.5])
subplot(1, 2, 1)
sigs = np.arange(.01, .5, .01)
bsv = np.array([f(s) for s in sigs])
plot(sigs, bsv, '-')
axhline(color = 'r');
xlabel('Volatility')
ylabel('Price');
title('Black Scholes Call')
subplot(1, 2, 2)
x2 = np.arange(-5, 5, .1)
plot(x2, f2(x2));
xlabel('$x$')
axhline(color = 'r');
xlim(-5, 5)
title('$\Phi(x) + .05x - 0.5 = 0$');

Bisection

• initial guess must bucket the solution: find $x\in [a,b]$ such that $f(x) = 0$, given
  • $f(a)*f(b) \leq 0$
• the function must be continuous
• converges to a root linearly (absolute error halves for each iteration).
  • $\epsilon_{n+1} \le c \epsilon_n^q, \;\epsilon_n = \left| x_n - x_{root}\right|,\; q=1, \;c=\frac{1}{2}$

import scipy.optimize as opt
a = .1
b = .45

def cumf (x, func, xs) :
    xs.append(x)
    return func(x)

xs = []
nx = opt.bisect(cumf, a, b, args=(f, xs))

def show_converge(f, xs, a, b, maxIter, tag, diagline = True, txty = .5) :
    figure(figsize = [12, 3.5])
    subplot(1, 2, 1)

    xr = np.arange(a*.9, b*1.1, (b-a)/500.)
    bsv = np.array(list(map(f, xr)))

    plot(xr, bsv, '-')
    axhline(color = 'k');

    for i in range(maxIter) :
        plot([xs[i], xs[i]], [0, f(xs[i])])
        scatter(xs[i], txty*(1. if f(xs[i]) < 0 else -1.), 
                s=150, marker = "$%d$"% i)
        if diagline and i< (maxIter-1):
            plot([xs[i], xs[i+1]], [f(xs[i]), 0])

    xlim(a*.9, b*1.1);
    ylim(f(a) - .2, f(b) + .2);
    xlabel('$x$')
    ylabel('$f(x)$')
    title(tag)

    subplot(1, 2, 2)
    es = np.abs(list(map(f, xs)))
    semilogy(es, '.');
    xlabel('Iterations')
    title('Error');
    
show_converge(f, xs, .1, .45, 6, 'Bisection', False)

Secant

• Uses the secant line to find successive approximation

$$ x_n = x_{n-1} - f(x_{n-1})\frac{x_{n-1} - x_{n-2}}{f(x_{n-1}) - f(x_{n-2})} $$

• Converges faster than Bisection method with $\epsilon_{n+1} \le c\epsilon_n^q, \; q\approx 1.618 $
• Can be thought of as poor man's choice of the Newton's method --- also referred to as a quasi-Newton method.

xs = []
g = lambda s, foo, bar : bs_vega(r=.05, s=100, k=150., sigma=s, t=1) 
nx = opt.newton(cumf, b, args=(f, xs))

show_converge(f, xs, 0.2, .45, 4, 'Secant', True)

• Secant method is not guaranteed to converge.
• Suffers for wiggly functions with small/vanishing derivative.

xs = []
try : 
    nx = opt.newton(cumf, 3, args=(f2, xs))
except RuntimeError:
    pass

show_converge(f2, xs, -11, 11, 5, 'Secant', True, .1)

Newton-Ralphson

• Use first derivative to approximate the root

$$ x_n = x_{n-1} - \frac{f(x_{n-1})}{f'(x_{n-1})} $$

• converges quadratically: $\epsilon_{n+1} \le c\epsilon_n^q,\; q=2$.

xs = []
nx = opt.newton(cumf, b, g, args=(f, xs))

show_converge(f, xs, 0.2, .45, 3, 'Newton-Ralphson', True)

• convergence is not guaranteed, it can fail around inflection point
• guaranteed convergence if the function is convex everywhere.

xs = []

try : 
    nx = opt.newton(cumf, 2, g2, args=(f2, xs))
except RuntimeError:
    pass

show_converge(f2, xs, -5, 9.5, 3, 'Newton-Ralphson', True, .1)

Brent

• An adaptive algorithm---mixes root bracketing, bisection and
• Inverse quadratic interpolation (Secant uses linear interpolation)
• Guaranteed to find a solution if initial guesses bucket the root
• Usually converges very fast $\epsilon_{n+1} \le c\epsilon_n^q, \; q \approx 1.839$.
• Often the default choice in practice

xs = []
g = lambda s, foo, bar : bs_vega(r=.05, s=100, k=150., sigma=s, t=1) 
nx = opt.brentq(cumf, a, b, args=(f, xs))

show_converge(f, xs, 0.1, .45, 5, 'Brent', False)

The challenging $\Phi(x) + .05x - 0.5 = 0$ converges under Brent:

xs = []
nx = opt.brentq(cumf, -1, 4, args=(f2, xs))

show_converge(f2, xs, -1.5, 5, 5, 'Brent', True, .1)

Interpolation

interpolate: verb, insert (something) between fixed points

Common interpolation methods

From a discrete set of knot values $x_i, y_i$, find a function $f: x \rightarrow y$.

• that hits all the knot values

Common interpolation methods:

• Linear
• Polynomial
• Cubic spline

We will cover in detail:

• Tension spline
• Maximum entropy (if time permits)

Linear interpolation

x = np.array([.1, 1.,2, 3., 5., 10., 25.])
y = np.array([.0025, .01, .016,.02, .025, .030, .035])
plot(x, y, '-o');
xlabel('Year')
ylabel('Rates');
title('Linear Interpolation');

Piecewise constant interpolation

• values equals to the observation to the right (or left).
• simple (maybe even silly) but useful in curve building
• works well with bootstrap

m = dict(zip(x, y))
m.update(dict(zip(x[:-1] + 1e-6, y[1:])))
k, v = zip(*sorted(m.items()))
plot(k, v, 'o-')
title('Piecewise Constant');

Polynomial interpolation

• Fit a polynomial function of order $n-1$ to the $n$ observations.
• The exact solution is known as the Lagrange polynomials:

$$ p(x) = \sum_{i=0}^n(\prod_{1\le j \le n, j\ne i}\frac{x-x_j}{x_i-x_j})y_i $$

It is rarely used in practice because ...

z = np.polyfit(x, y, len(x)-1)
p = np.poly1d(z)
x1d = arange(0, 26, .1)
plot(x1d, p(x1d))
plot(x, y, 'o');
title('Polynomial');

Spline interpolation

Spline is an elastic string or pipe, used by draftsmen to draw smooth curves through fixed knots before the computer age:

Spline interpolation is a mathematical model for the physical spline.

Cubic spline

Cubic spline uses a 3rd order polynomial for each line section between knots

$$q_i(x) = a_i + b_i x + c_i x^2 + d_i x^3 \;,\;\; x_i < x < x_{i+1}$$

Enforce continuity up to the 2nd derivatives:

\begin{eqnarray} q_{i-1}(x_i) &=& q_{i}(x_i) \\ q'_{i-1}(x_i) &=& q'_{i}(x_i) \\ q''_{i-1}(x_i) &=& q''_{i}(x_i) \end{eqnarray}

Boundary conditions

For $n$ knots, there are $n-1$ line sections with $4(n-1)$ parameters

• $n$ constraint for the hitting the $n$ knot values
• 3 continuity constraints for each intermediate knot: $3(n-2)$
• $4n-6$ constraints in total

Two additional constraints required to uniquely determine the cubic spline:

• Natural Spline: $s''_1(x_1) = s''_{n-1}(x_{n}) = 0$
• End slope conditions: $s'_1(x_1) = c_0, s'_{n-1}(x_{n}) = c_1$

Cubic spline examples

Spline interpolation is very smooth

However, it does not preserve monotonicity and convexity

• it could overshoot
• can result in arbitrages in many situations

import lin

ts = lin.RationalTension(0.)
ts.build(x, y)

x2 = np.array([.01, .03, .07, .1, .6])
y2 = np.array([.0095, .023, .035, .040, .042])

figure(figsize=[12, 4])
subplot(1, 2, 1)
plot(x1d, ts.value(x1d))
plot(x, y, 'o');
title('Cubic Spline');

subplot(1, 2, 2)
ts.build(x2, y2)
x2d = arange(.01, .65, .01)
plot(x2d, ts.value(x2d))
plot(x2, y2, 'o');
xlabel('Detachement')
title('CDO Tranche Expected Loss');

Convexity

Option-like instruments' prices are convex functions:

$$ v(k) = \mathbb{E}[\max(\tilde s - k, 0)] $$

No arbitrage requires $\frac{\partial^2 v}{\partial k^2} > 0 $, because:

$$\small \frac{\partial^2}{\partial k^2}\mathbb{E}[\max(\tilde s-k, 0)] = \mathbb{E}[\frac{\partial^2}{\partial k^2} \max(\tilde s-k, 0)] = \mathbb{E}[\delta(\tilde s-k)] = p(k) $$

• $\delta(x)$ is the Dirac delta function: $\int_{-\infty}^{\infty} f(x) \delta(x-a) dx = f(a)$
• $p(\cdot)$ is the probability density function of $\tilde s$
• The expected loss of a 0 to $k$ tranche is concave because:
  • $v(k) = \mathbb{E}[\min(\tilde l, k)] = k - \mathbb{E}[\max(k-\tilde l, 0)]$

Exponential tension spline

A tension spline is originally defined as: $f^{(4)}(x) - \lambda f''(x) = 0$

• it models a physical spline stretched by a tension force
• $\lambda$ is the ratio of the tension force over the rigidity of the spline
• it reduces to cubic spline when $\lambda = 0$
• with $\lambda \rightarrow \infty$, the spline is stretched to piece-wise straight lines
• the solution is a combination of exponential and linear functions of $x$

Rational tension spline

Generic tension spline has the following property:

• has a scalar tension parameter $\lambda$
• when $\lambda = 0$, it reduces to cubic spline
• it converges to piecewise linear interpolation uniformly as $\lambda$ increases

Rational tension spline is a convenient form of generic tension spline:

import fmt

a, b, c, d, t = sp.symbols('a b c d t', real = True)
l = sp.symbols('lambda', positive=True)
f = sp.Function('f')
df = sp.Function("\dot{f}")
ddf = sp.Function("\ddot{f}")

r = (a + b*t + c*t**2 + d*t**3)/(1 + l*t*(1-t))
s_x, xi, xii, xi_ = sp.symbols('x, x_i, x_{i+1}, x_{i-1}', real=True)

fmt.displayMath(fmt.joinMath('=', f(t), r), fmt.joinMath('=', t, (s_x-xi)/(xii-xi)))

$$ f{\left (t \right )}=\frac{a + b t + c t^{2} + d t^{3}}{\lambda t \left(- t + 1\right) + 1}\;,\;\;\;t=\frac{x - x_{i}}{- x_{i} + x_{i+1}}$$

• it is more tractable than the exponential tension spline as only polynomial functions are involved
• solvable the same way as cubic spline, $\lambda$ is a known parameter

Constraints

The rationale tension spline's values and derivatives at $t=0$ and $t=1$:

from fmt import math2df
pd.options.display.max_colwidth=300

def lincollect(e, tms) :
    m = sp.collect(sp.expand(e), tms, evaluate=False)
    return [m[k] if k in m else 0 for k in tms]

coefs = sp.Matrix([a, b, c, d])
drt0 = sp.Matrix([lincollect(r.diff(t, i).subs({t:0}), coefs) for i in range(3)])
drt1 = sp.Matrix([lincollect(r.diff(t, i).subs({t:1}), coefs) for i in range(3)])

derivs = sp.Matrix([f(t), df(t), ddf(t)])
fmt.displayMath(fmt.joinMath('=', derivs.subs({t:0}), drt0), coefs, sep="", pre="\\scriptsize")
fmt.displayMath(fmt.joinMath('=', derivs.subs({t:1}), drt1), coefs, sep="", pre="\\scriptsize")

$$\scriptsize \left(\begin{matrix}f{\left (0 \right )}\\\dot{f}{\left (0 \right )}\\\ddot{f}{\left (0 \right )}\end{matrix}\right)=\left(\begin{matrix}1 & 0 & 0 & 0\\- \lambda & 1 & 0 & 0\\2 \lambda^{2} + 2 \lambda & - 2 \lambda & 2 & 0\end{matrix}\right)\left(\begin{matrix}a\\b\\c\\d\end{matrix}\right)$$

$$\scriptsize \left(\begin{matrix}f{\left (1 \right )}\\\dot{f}{\left (1 \right )}\\\ddot{f}{\left (1 \right )}\end{matrix}\right)=\left(\begin{matrix}1 & 1 & 1 & 1\\\lambda & \lambda + 1 & \lambda + 2 & \lambda + 3\\2 \lambda^{2} + 2 \lambda & 2 \lambda^{2} + 4 \lambda & 2 \lambda^{2} + 6 \lambda + 2 & 2 \lambda^{2} + 8 \lambda + 6\end{matrix}\right)\left(\begin{matrix}a\\b\\c\\d\end{matrix}\right)$$

• Note the short-handed notation of $\ddot{f}(1) = \frac{d^2f(t)}{d t^2} \rvert _{t=1}$ etc.
• $\lambda$ is a known constant
• Like cubic spline, there are $4(n-1)$ variables and constraints
• Solvable as a $4(n-1)$ dimensional linear systems ~ $O((4n)^3)$

A better solution

Consider one line section between $[x_i, x_{i+1}]$:

• the four coefficients are fully determined by $f(0)$, $f(1)$, $\ddot{f}(0)$, $\ddot{f}(1)$:

s_v = sp.Matrix([f(0), f(1), ddf(0), ddf(1)])
s_a = sp.Matrix([drt0[0, :], drt1[0, :], drt0[2, :], drt1[2, :]])

fmt.displayMath(s_a, fmt.joinMath('=', coefs, s_v), sep="", pre="\\scriptsize")

$$\scriptsize \left(\begin{matrix}1 & 0 & 0 & 0\\1 & 1 & 1 & 1\\2 \lambda^{2} + 2 \lambda & - 2 \lambda & 2 & 0\\2 \lambda^{2} + 2 \lambda & 2 \lambda^{2} + 4 \lambda & 2 \lambda^{2} + 6 \lambda + 2 & 2 \lambda^{2} + 8 \lambda + 6\end{matrix}\right)\left(\begin{matrix}a\\b\\c\\d\end{matrix}\right)=\left(\begin{matrix}f{\left (0 \right )}\\f{\left (1 \right )}\\\ddot{f}{\left (0 \right )}\\\ddot{f}{\left (1 \right )}\end{matrix}\right)$$

The linear system can be explicitly inverted (by sympy!):

ss = sp.simplify(sp.expand(s_a.inv()))
fmt.displayMath(fmt.joinMath('=', coefs, ss), s_v, sep="\\scriptsize")

$$ \left(\begin{matrix}a\\b\\c\\d\end{matrix}\right)=\left(\begin{matrix}1 & 0 & 0 & 0\\\lambda - 1 & 1 & - \frac{\lambda + 2}{2 \lambda^{2} + 8 \lambda + 6} & - \frac{1}{2 \lambda^{2} + 8 \lambda + 6}\\- 2 \lambda & \lambda & \frac{\lambda + \frac{3}{2}}{\lambda^{2} + 4 \lambda + 3} & - \frac{\lambda}{2 \lambda^{2} + 8 \lambda + 6}\\\lambda & - \lambda & - \frac{1}{2 \lambda + 6} & \frac{1}{2 \left(\lambda + 3\right)}\end{matrix}\right)\scriptsize\left(\begin{matrix}f{\left (0 \right )}\\f{\left (1 \right )}\\\ddot{f}{\left (0 \right )}\\\ddot{f}{\left (1 \right )}\end{matrix}\right)$$

• the resulting $a, b, c, d$ ensures that the rational tension spline hits the target $f(t), \ddot{f}(t)$ at both ends of the line section.
• $\dot{f}(x_i)$ becomes linear combinations of $f$ and $\ddot f$ for line sections $[x_{i-1}, x_i]$ or $[x_i, x_{i+1}]$
  • the $\dot{f}(x_i)$ from the left and right line sections must equal

Continuity conditions

Thus $\ddot{f}(x_i)$ at the knots are the only $n$ unknowns, which are solvable from the following $n$ constraints:

• End condition (natural spline): $\ddot{f}(x_1) = \ddot{f}(x_{n}) = 0$
• Continuity in $\dot{f}(x_i)$ for $n-2$ intermediate knots

Note that $f(\cdot)$ and its derivatives are continuous in $x$, not $t$:

$$ \frac{d^k f(t)}{dt^k} = (x_{i+1}-x_i)^k\frac{d^k f(x)}{dx^k} $$

• this is because $t = \frac{x-x_i}{x_{i+1} - x_i}$
• what if end conditions are given in $\dot{f}(x_1)$ and $\dot{f}(x_{n})$?

Continuity in $f'(x_i)$

xl, xr = sp.symbols('x_l, x_r')
vm = {xl:(xi-xi_), xr:(xii-xi)}

sl = sp.Matrix([f(xi_), f(xi), ddf(xi_)*xl**2, ddf(xi)*xl**2])
sr = sp.Matrix([f(xi), f(xii), ddf(xi)*xr**2, ddf(xii)*xr**2])
dl = sp.simplify(sp.expand((drt1[1,:]*ss*sl/xl)[0,0]))
dr = sp.simplify(sp.expand((drt0[1,:]*ss*sr/xr)[0,0]))

terms = sp.Matrix([ddf(xi_), ddf(xi), ddf(xii)])
d1 = sp.collect(sp.expand(dl - dr), terms, evaluate=False)

mr = sp.Matrix([sp.simplify(sp.simplify(d1[k]).subs(vm)) for k in terms])
rhs = sp.simplify(-d1[sp.S.One]).subs(vm)
fmt.displayMath(mr.T, terms, sep="")
fmt.displayMath("\;\;\;\;\;\;\; =", rhs, sep="")
#displayMath(*[fmt.joinMath('=', k, v) for k, v in vm.items()])

$$ \left(\begin{matrix}\frac{x_{i} - x_{i-1}}{2 \left(\lambda^{2} + 4 \lambda + 3\right)} & \frac{\frac{\lambda x_{i+1}}{2} - \frac{\lambda x_{i-1}}{2} + x_{i+1} - x_{i-1}}{\lambda^{2} + 4 \lambda + 3} & \frac{- x_{i} + x_{i+1}}{2 \left(\lambda^{2} + 4 \lambda + 3\right)}\end{matrix}\right)\left(\begin{matrix}\ddot{f}{\left (x_{i-1} \right )}\\\ddot{f}{\left (x_{i} \right )}\\\ddot{f}{\left (x_{i+1} \right )}\end{matrix}\right)$$

$$ \;\;\;\;\;\;\; =- \frac{f{\left (x_{i} \right )}}{x_{i} - x_{i-1}} + \frac{f{\left (x_{i-1} \right )}}{x_{i} - x_{i-1}} - \frac{f{\left (x_{i} \right )}}{- x_{i} + x_{i+1}} + \frac{f{\left (x_{i+1} \right )}}{- x_{i} + x_{i+1}}$$

• this linear system can be written as a tri-diagonal matrix

Tri-diagonal system

The following is the linear system of the 1st interpolation example with $\lambda = 2$:

import trid
ts3 = trid.TridiagTension(2.)
ts3.build(x, y)

fmt.displayMath(sp.Matrix(np.round(ts3.a, 3)), fmt.joinMath('=', "\\boldsymbol{\\ddot{f}}", #ddf(s_x), 
                sp.Matrix(np.round(ts3.b, 4))), sep="", pre="\\small")

$$\small \left(\begin{matrix}1.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\0.03 & 0.253 & 0.033 & 0.0 & 0.0 & 0.0 & 0.0\\0.0 & 0.033 & 0.267 & 0.033 & 0.0 & 0.0 & 0.0\\0.0 & 0.0 & 0.033 & 0.4 & 0.067 & 0.0 & 0.0\\0.0 & 0.0 & 0.0 & 0.067 & 0.933 & 0.167 & 0.0\\0.0 & 0.0 & 0.0 & 0.0 & 0.167 & 2.667 & 0.5\\0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 1.0\end{matrix}\right)\boldsymbol{\ddot{f}}=\left(\begin{matrix}0.0\\-0.0023\\-0.002\\-0.0015\\-0.0015\\-0.0007\\0.0\end{matrix}\right)$$

Thomas algorithm:

• a sparse version of the LU decomposition
• solves the tri-diagonal system in $O(n)$ operations

What is the complexity of regular LU decomposition?

Tension spline examples

def plotTension(x, y, lbds, xd) :
    plot(x, y, 'o');
    title('Tension Spline');

    for lbd in lbds:
        ts = lin.RationalTension(lbd)
        ts.build(x, y)
        plot(xd, ts.value(xd))
    
    legend(['data'] + ['$\lambda = %.f$' % l for l in lbds], loc='best');

lbds = (0, 2, 10, 50)

figure(figsize=[12, 4])
subplot(1, 2, 1)
plotTension(x, y, lbds, x1d)
subplot(1, 2, 2)
plotTension(x2, y2, lbds, x2d)

• converges to piece wise flat curve uniformly with increasing $\lambda$

Perturbation locality

Spline interpolation is global:

• changing a single knot affects the whole curve
• the perturbation is more localized with greater tension parameter $\lambda$

def plotPerturb(x, y, yp, xd, lbds) :
    plot(x, yp-y, 'o')
    for lbd in lbds:
        ts = lin.RationalTension(lbd)
        ts.build(x, y)
        tsp = lin.RationalTension(lbd)
        tsp.build(x, yp)

        plot(xd, tsp.value(xd) - ts.value(xd))
        
    xlabel('$x$')
    ylabel('$y$')
    title('Changes in Spline')
    legend(['knots'] + ['$\lambda = %.f$' % l for l in lbds], loc='best');

dy = .01
figure(figsize=[12, 4])
subplot(1, 2, 1)
idx = 3
yp = np.copy(y)
yp[idx] *= 1. + dy

plotPerturb(x, y, yp, x1d, lbds)

subplot(1, 2, 2)
idx = 1
yp = np.copy(y2)
yp[idx] *= 1. + dy
plotPerturb(x2, y2, yp, x2d, lbds)

Integral of tension spline

• Though complicated, the integral is analytical nonetheless
• The integral can be useful in deriving analytical pricing formulae
  • derived using sympy

s_s0, s_s1, s_s2, s_c1, s_c2, s_com = sp.symbols('s_0, s_1, s_2, c_1, c_2, c_0')
short = sp.simplify(sp.Rational(1, 2)/l/s_com*(s_s0 + s_s1*(s_c1 + s_c2) + s_s2*(s_c1 - s_c2)))
fmt.displayMath(fmt.joinMath('=', sp.Integral(r, (t, 0, tt)), short), pre="\\scriptsize ")

com = sp.sqrt(l*(l+4))

s0 = -d*tt**2*s_com - 2*tt*(c+d)*s_com
s1 = sp.log((sp.sqrt(l+4)+sp.sqrt(l))/(sp.sqrt(l+4)+sp.sqrt(l)-2*sp.sqrt(l)*tt))
s2 = sp.log((sp.sqrt(l+4)-sp.sqrt(l))/(sp.sqrt(l+4)-sp.sqrt(l)+2*sp.sqrt(l)*tt))

c1 = d*s_com/l + s_com*(b+c+d)
c2 = l*(2*a+b+c+d)+(2*c+3*d)

#short = sp.simplify(sp.Rational(1, 2)/l/com*(s0 + s1*(c1 + c2) + s2*(c1 - c2))).subs({s_com:com})

fmt.displayMath(fmt.joinMath('=', s_com, com), fmt.joinMath('=', s_s0, s0), pre="\\scriptsize ")
fmt.displayMath(fmt.joinMath('=', s_s1, s1), fmt.joinMath('=', s_s2, s2), pre="\\scriptsize ")
fmt.displayMath(fmt.joinMath('=', s_c1, c1), fmt.joinMath('=', s_c2, c2), pre="\\scriptsize ")

$$\scriptsize \int_{0}^{\tau} \frac{a + b t + c t^{2} + d t^{3}}{\lambda t \left(- t + 1\right) + 1}\, dt=\frac{1}{2 c_{0} \lambda} \left(s_{0} + s_{1} \left(c_{1} + c_{2}\right) + s_{2} \left(c_{1} - c_{2}\right)\right)$$

$$\scriptsize c_{0}=\sqrt{\lambda} \sqrt{\lambda + 4}\;,\;\;\;s_{0}=- c_{0} d \tau^{2} - 2 c_{0} \tau \left(c + d\right)$$

$$\scriptsize s_{1}=\log{\left (\frac{\sqrt{\lambda} + \sqrt{\lambda + 4}}{- 2 \sqrt{\lambda} \tau + \sqrt{\lambda} + \sqrt{\lambda + 4}} \right )}\;,\;\;\;s_{2}=\log{\left (\frac{- \sqrt{\lambda} + \sqrt{\lambda + 4}}{2 \sqrt{\lambda} \tau - \sqrt{\lambda} + \sqrt{\lambda + 4}} \right )}$$

$$\scriptsize c_{1}=\frac{c_{0} d}{\lambda} + c_{0} \left(b + c + d\right)\;,\;\;\;c_{2}=2 c + 3 d + \lambda \left(2 a + b + c + d\right)$$

Curve Building in Finance

In life, as in art, the beautiful moves in curves.

Curve building fundamentals

• Inputs: prices of benchmark instruments of the same risk factor, at different maturities
• Outputs: a single curve for the underlying factor that explains all observed prices to adequate precision.
• Curve building is a fundamental problem in Finance, it can become extremely complicated

Common types of curves

• Interest rate: OIS, Libor 3M/6M etc,
• CDS (credit default swap)
• Commodity
• FX
• Inflation

Curve terminology

$b(t)$ is the price of risk free zero coupon bond maturing at $t$:

• Zero rate (or spot rate, yield, internal rate of return):

$$r(t) = -\frac{1}{t}\log(b(t)) \iff b(t) = e^{-r(t) t} $$

• Forward rate:

$$f(t) = -\frac{1}{b(t)}\frac{d b(t)}{d t} \iff b(t) = e^{-\int_{0}^t f(s) ds} $$

• Swap rate (continuous coupon):

$$s(t) = \frac{1 - b(t)}{\int_0^t b(s) ds} \iff s(t) \int_0^t b(s) ds + b(t) = 1 $$

Relationship between rates

dt = .1
t = np.arange(dt, 30, dt)

tn = np.array([0, 5, 30])
rn = np.array([.04, .06, .055])

cv = lin.RationalTension(2.)
cv.build(tn, rn)

f = cv(t) + t*cv.deriv(t)
b = exp(-t*cv(t))
intb = np.cumsum(b*dt)
s = (1-b)/intb

plot(t, cv(t));
plot(t, f)
plot(t, s)

legend(['Zero Rate', 'Forward Rate', 'Swap Rate'], loc='best');
xlabel('Time');

• zero rate is the average of forward rate:

$$ r(t) = \frac{1}{t} \int_0^t f(s) ds $$

• zero rate is an approximation to the swap rate (when $b(t) \approx 1$):

$$ s(t) = \frac{1 - b(t)}{\int_0^t b(s) ds} \approx \frac{1 - e^{-r(t)t}}{t} \approx \frac{r(t) t}{t} = r(t) $$

Introduction to CDS

No Default	With Default

CDS is an insurance against a reference entity's default risk

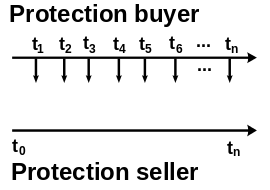
• protection buyer: makes quarterly payments of notional$\times$spread$\times$daycount.
• protection seller: pays the default loss of notional$\times$(1-rec) when the reference entity defaults before CDS maturity.

Long or short ?

Important market convention: long position is always equivalent to owning the underlying bond

• receiver swap is long $\iff$ own a fixed coupon risk free bond
• sell CDS protection is long $\iff$ own a fixed coupon risky bond

Deltas are always communicated by perturbing the market to the longer side, i.e., the direction where long positions makes money:

• interest rate decrease by 1bps
• credit spread compress by 1bps
• positive deltas always corresponds to long positions

Often the risk computation is done by bumping rates +1bps, then flipping the signs before the final reporting.

IR vs credit terminologies

In a very loose way, the following terms are the counterparts between IR and credit/CDS market (all in continuous compounding):

	Interest Rate	Credit
primary state variable	discount factor $b(t)$	survival probability $p(t)$
yield, IRR	zero rate $r(t) = -\frac{1}{t}\log(b(t))$	quoted spread $q(t) \approx -\frac{1 - \text{rec}}{t}\log(p(t))$
forward rate	forward interest rate $f(t) = -\frac{1}{b(t)}\frac{d b(t)}{d t} $	hazard rate $h(t) = -\frac{1}{p(t)}\frac{d p(t)}{d t} $
par swap rate $s(t)$	par IR swap rate	par CDS spread
cumulative yield	$y(t) = -\log(b(t))$	$g(t) = -\log(p(t)) $

CDS benchmark instruments

The following is a representative set of CDS quotes observed in the market:

import inst

def flatCurve(rate) :
    return lambda t : np.exp(-rate*t)

disc = flatCurve(.01)

terms = np.array([.25, .5, 1., 2, 3, 4, 5, 6, 7, 8, 10])
qs = np.array([80, 85, 95, 154, 222, 300, 385, 410, 451, 470, 480])

cps = np.ones(len(terms))*100
insts = [inst.CDS(m, c*1e-4, .4) for m, c in zip(terms, cps)]

#compute the upfront PV of the benchmark instruments
ufr = np.array([i.pv01(disc, flatCurve(f*1e-4))*(c-f)*1e-4 for i, f, c in zip(insts, qs, cps)])

mat_tag = 'Maturity (Y)'
pd.set_option('precision', 4)

cds_data = pd.DataFrame({mat_tag:terms, 'Coupon(bps)':cps, 'Quoted Spread(bps)':qs, 'PV (% Points)': ufr*100.}).set_index(mat_tag)
fmt.displayDF(cds_data.T, "4g", fontsize=2)
benchmarks = dict(zip(insts, ufr))

Maturity (Y)	0.25	0.5	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0	10.0
Coupon(bps)	100	100	100	100	100	100	100	100	100	100	100
Quoted Spread(bps)	80	85	95	154	222	300	385	410	451	470	480
PV (% Points)	0.04978	0.07448	0.0494	-1.05	-3.475	-7.356	-12.58	-15.92	-20.25	-23.6	-28.63

• the CDS contract have standardised semi-annual maturities, on Mar-20 and Sep-20
• it usually costs more per annum for longer term contracts
• for most names, there are only a few liquid CDS instruments, referred as the benchmark instruments
• quoted spreads is a way to communicate the upfront payment, it loosely corresponds to the zero rate or yield in IR

What to interpolate?

It is important to choose the right quantity to interpolate

• There are many potential choices, e..g: $f(t), f'(t)$ or $\int_0^t f(s) ds$ etc.
• Which variable is a natural fit for tension spline's stretch operation?
• We want the variable itself to be continuous, but can live with the discontinuities in $f'(t)$ when $\lambda \rightarrow \infty$

Industry standard: $$p(t) = e^{-\int_0^t h(s) ds}$$

• build piecewise flat curve in hazard rate $h(t)$ for CDS:
• where $p(t)$ is the survival probability of the reference entity at time $t$.

this is quite odd, why don't we use a continuous interpolation in $h(t)$?

• such as piece wise linear or cubic spline?

Triangular dependency

The objective:

• build a curve in hazard rate $\bs h(t)$ that exactly reproduce all observed CDS prices quoted in $\bs q(t)$

	$h(3m)$	$h(6m)$	$h(1Y)$	$h(2Y)$	$h(5Y)$
$q(3m)$	X
$q(6m)$	*	X
$q(1Y)$	*	*	X
$q(2Y)$	*	*	*	X
$q(5Y)$	*	*	*	*	X

Bootstrap is the standard method to build curves with triangular dependency:

• Solve the knot values one by one, using benchmark instruments with increasing maturities

Piecewise flat bootstrap

• This is the standard approach to build CDS curves in the industry
• $g(t)$ is the cumulative hazard: $g(t) = \int_0^t h(s) ds = -\log(p(t))$
• Piecewise flat in hazard rate $h(t)$ is equivalent to piecewise linear in $g(t)$

cdspv = inst.cdspv(disc, inst.zero2disc)

hlin = lin.PiecewiseLinear()
hlin.build(terms, terms*.01)
hlin.addKnot(0, 0)
hlin = inst.bootstrap(benchmarks, hlin, cdspv, bds = [-1., 1.])
cds_data['PV Error (bps) - Linear'] = np.round([1e4*(cdspv(i, hlin) - benchmarks[i]) for i in insts], 4)

xs = np.arange(.01, 10, .01)

figure(figsize=[12, 4])
subplot(1, 2, 1)
plot(xs, hlin(xs))
plot(terms, hlin(terms), 'o')
xlabel('Time')
title('$g(t)$');

subplot(1, 2, 2)
plot(xs, hlin.deriv(xs))
plot(terms, hlin.deriv(terms-1e-4), 'o')
xlabel('Time')
title('$h(t)$');

Pros and cons of piecewise flat bootstrap

• All benchmark prices are exactly matched, after bootstrap with piecewise flat hazard rate.
• Discontinuity in hazard rate causes hedging problems, risk profiles jump over the roll dates.

fmt.displayDF(cds_data.T, "4g", fontsize=2)

Maturity (Y)	0.25	0.5	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0	10.0
Coupon(bps)	100	100	100	100	100	100	100	100	100	100	100
Quoted Spread(bps)	80	85	95	154	222	300	385	410	451	470	480
PV (% Points)	0.04978	0.07448	0.0494	-1.05	-3.475	-7.356	-12.58	-15.92	-20.25	-23.6	-28.63
PV Error (bps) - Linear	-0	-0	-0	-0	-0	-0	0	0	-0	-0	-0

How to remove the discontinuity in hazard rate?

• applying cubic spline to hazard rate seems to be a natural idea, does it work?

Cumulative hazard

The cumulative hazard $g(t)$ is a suitable variable for the tension spline interpolation:

$$g(t) = \int_0^t h(s) ds = -\log(p(t))$$

• $g(t)$ is continuous and monotonic, 1 to 1 with $p(t)$
• $g(0) = 0$, the boundary condition is well defined
• $h(t) = g'(t)$ can be discontinuous when $\lambda \rightarrow \infty$, this reverts to the standard method of piecewise flat hazard rate
• with finite $\lambda$, hazard rate is smooth and continuous

This argument carries over to the interest rate curve building:

• the cumulative yield, $y(t) = -\log(b(t))$, is a suitable variable to apply tension spline

Bootstrap with tension spline

def plotboot(tsit, lbd, ax, tagsf) :
    xlabel('Time')    
    
    lbd_tag = '$\\lambda=%.f$' % lbd
    df = pd.DataFrame({'$t$':xs}).set_index(['$t$'])
    
    for tag, f in tagsf :
        df[tag] = f(tsit, xs) 
    
    df.plot(ax = ax, secondary_y = [tagsf[0][0]], title = 'Tension Spline ' + lbd_tag)
    plot(terms, tsit(terms), 'o')

tagsf = [("$g(t)$", lambda cv, xs : cv(xs)), ("$h(t)$", lambda cv, xs : cv.deriv(xs))]

lbds = [0, 2, 10, 100]
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=[12, 8])

es = []

for lbd, ax in zip(lbds, axes.flatten()) :
    tsit, e = inst.iterboot(benchmarks, cdspv, lbd=lbd, x0=0, its=1)
    plotboot(tsit, lbd, ax, tagsf)  
    es.append(e[0])

Bootstrapping with global interpolation

The benchmark CDS won't reprice exactly after the bootstrapping with tension spline:

• Changes in longer maturity affects the shorter end of the curve
• The dependency matrix is no longer triangular, but close

df = pd.DataFrame(np.array(es)*1e4, index=['Fit Error (bps) $\\lambda$=%g' % l for l in lbds], 
                  columns = ['%gY' % t for t in terms])
fmt.displayDF(df, "4f", fontsize=2)

	0.25Y	0.5Y	1Y	2Y	3Y	4Y	5Y	6Y	7Y	8Y	10Y
Fit Error (bps) $\lambda$=0	-0.0000	-0.0000	0.0352	0.7148	1.1093	1.9968	2.1802	2.6090	2.5612	0.8231	0.0000
Fit Error (bps) $\lambda$=2	-0.0000	-0.0000	0.0232	0.4637	0.7908	1.2876	1.4579	1.7260	1.7838	0.6388	0.0000
Fit Error (bps) $\lambda$=10	-0.0000	-0.0000	0.0098	0.2026	0.3602	0.5634	0.6458	0.7598	0.8039	0.3038	-0.0000
Fit Error (bps) $\lambda$=100	-0.0000	-0.0000	0.0013	0.0281	0.0507	0.0782	0.0900	0.1057	0.1128	0.0435	0.0000

Recall how we force matrix to be triangular using QR algorithm?

Iterative algorithm

Iteration is an effective method for near triangular dependency:

$$\bs x^{i+1} = f(\bs x^i)$$

• where $f(\cdot)$ represent the bootstrap operation, $\bs x^i$ is knot solutions
• $\bs x^0$ is a initial guess, e.g. a flat curve
• simple and effective, usually outperforms sophisticated optimizers

Iteration with mixing

Mixing the old and new results between iterations improves stability:

$$\bs x^{i+1} = m f(\bs x^i) + \left(1-m\right) \bs x^i$$

• $m = 0.5$ is often a good choice

figure(figsize=[12, 4])
ax = subplot(1, 2, 1)

tsit, e = inst.iterboot(benchmarks, cdspv, x0=0, lbd = lbds[0], its=6)
tsit1, e1 = inst.iterboot(benchmarks, cdspv, x0=0, lbd = lbds[0], mixf=0.5, its=6)

plotboot(tsit, lbds[0], ax, tagsf)    

subplot(1, 2, 2)
semilogy(range(1, len(e)+1), np.transpose([np.linalg.norm(e, 2, 1)*1e4, np.linalg.norm(e1, 2, 1)*1e4]), 'o-')
legend(['no mixing $m=0$', 'mixing $m=0.5$'], loc='best')

xlabel('Iteration')
ylabel('bps')
title('L-2 norm of error (bps)');

Effects of tension parameter $\lambda$

• No visible difference in $g(t)$
• Big difference in the hazard rate $h(t)$
  • the smaller $\lambda$, the smoother the $h(t)$

def pv_lbds(bms, cdspv, lbds, x0) :
    cvs = []
    for lbd in lbds:
        cv, e = inst.iterboot(bms, cdspv, x0, lbd, mixf = 0.5)
        cvs.append(cv)
    
    return cvs

lbds = (0, 2, 10, 50)
tags = ['$\\lambda=%.f$' % l for l in lbds]
cv0 = pv_lbds(benchmarks, cdspv, lbds, 0)

figure(figsize=[12, 4])
subplot(1, 2, 1)
plot(xs, np.array([cv(xs) for cv in cv0]).T);
title('$g(t)$')
xlabel('$t$')

subplot(1, 2, 2)
plot(xs, np.array([cv.deriv(xs) for cv in cv0]).T);
legend(tags, loc='best');
title('$h(t)$');
xlabel('$t$');

Perturbation locality

Changes in hazard rates are more localized with larger $\lambda$

• A highly desirable property in practice

def showPerts(bms, bms_ps, cdspv, lbds, x0, pertf) :
    cv0 = pv_lbds(bms, cdspv, lbds, x0=x0)
    cvp1, cvp2 = [pv_lbds(b, cdspv, lbds, x0=x0) for b in bms_ps]
    
    lbd_tags = ['$\\lambda=%.f$' % lbd for lbd in lbds]

    figure(figsize=[12, 4])

    subplot(1, 2, 1)
    plot(xs, 1e4*np.array([pertf(f, g)(xs) for f, g in zip(cv0, cvp1)]).T);
    xlabel('Tenor')
    ylabel('$\Delta h(t)$ (bps)')
    title('1bps Spread Perturbation @t=%.2f' % pts[0])
    legend(lbd_tags, loc='best');
    plot(terms, 1e4*np.array([pertf(f, g)(terms) for f, g in zip(cv0, cvp1)]).T, '.');

    subplot(1, 2, 2)
    plot(xs, 1e4*np.array([pertf(f, g)(xs) for f, g in zip(cv0, cvp2)]).T);
    xlabel('Tenor')
    ylabel('$\Delta h(t)$ (bps)')
    title('1bps Spread Perturbation @t=%.2f' % pts[1])
    legend(lbd_tags, loc='best');
    plot(terms, 1e4*np.array([pertf(f, g)(terms) for f, g in zip(cv0, cvp2)]).T, '.');
    
    
pts = [.5, 5]
bms_ps = [{k if k.maturity != pt else inst.CDS(k.maturity, k.coupon-1e-4, k.recovery) : v 
        for k, v in benchmarks.items()} for pt in pts]
    
showPerts(benchmarks, bms_ps, cdspv, lbds, 0, lambda f, g : lambda xs : f.deriv(xs) - g.deriv(xs))

Interpolate the hazard rate?

The result is disastrous:

• When $\lambda \rightarrow \infty$, it approaches linear interpolation in the hazard rate
• Linearly interpolating $h(t)$ leads to zigs and zags

hazard_pv = inst.cdspv(disc, inst.fwd2disc)
x0 = .01
chartf = [('$h(t)$',  lambda cv, xs : cv(xs)), ('H(t)', lambda cv, xs : cv.integral(xs))]

fig, axes = plt.subplots(nrows=1, ncols=2, figsize=[12, 4])

lbds = (0, 20)
tsit0, e0 = inst.iterboot(benchmarks, hazard_pv, x0, lbds[0], mixf=.5)
plotboot(tsit0, lbds[0], axes[0], chartf)    

tsit1, e1 = inst.iterboot(benchmarks, hazard_pv, x0, lbds[1], mixf=.5)
plotboot(tsit1, lbds[1], axes[1], chartf) 

Perturbation in a single tenor generates waves throughout the hazard rate term structure.

showPerts(benchmarks, bms_ps, hazard_pv, lbds, x0, lambda f, g : lambda xs : f(xs) - g(xs))

State variable

Generally, it is always better to interpolate the state variable:

• state variable is the primary determinant of the benchmark price, such as the cumulative hazard $g(t) = -\log(p(t))$
• the derivatives, like $h(t) = g'(t)$, only changes the prices through its cumulative effects (integral), which leads to zigzags and waves when combined with a continuous interpolation.

bootstrap derivative variables + continuous interpolation = DISASTER

Assignments

Recommended reading:

• Bindel and Goodman: Chapter 6.1, 6.2, 7.1

• Andersen and Piterbarg: Chapter 6.1-6.2, 6.A

Homework:

• Complete homework set 4